물리, 수학적 처리를 하다보면, 점과 선분 사이의 거리를 구해야 할 때가 있다.
직선과 점의 거리와는 다르게 선분과 점 사이의 거리는 조금 더 까다롭다.
아무튼 중고등학생 때의 기억을 되짚어보면서 구현 해 보았다.
1. 원리 이해
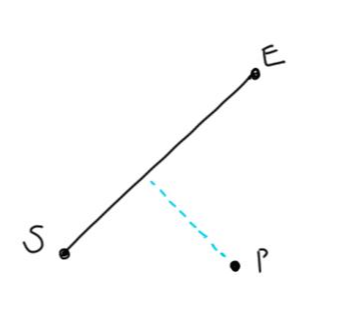

선분 SE, 점 P가 있다. 우선 점 P를 SE로 수선의 발을 내렸을 때, 그 안에 포함 되는지, 아니면 밖에 있는지 구분해야 한다.
이것을 구분하기 위해선, 벡터의 내적을 이용해야한다.
- 내적 > 0 이면, θ < 90
- 내적 < 0 이면, θ > 90
- 내적 = 0 이면,

위 그림과 같이, 점 P의 수선의 발이 선분 SE에 있는 경우, 벡터의 외적을 이용해 구할 수 있다. 벡터 외적의 크기는 두 벡터의 평행사변형 넓이이다.
벡터 SE와 벡터 SP의 외적의 크기 = (선분SE 길이) * (선분SE와 점 P의 거리)
즉
(벡터 SE와 벡터 SP의 외적의 크기)/(선분SE 길이) = (선분SE와 점 P의 거리)
이다.
남은 건 코드 뿐,
// 2차원 벡터 내적
public static float DotProduct(jdVector2 left, jdVector2 right)
{
return (float)(left.x* right.x + left.y* right.y);
}
// 2차원 벡터 외적
public static float CrossProduct(jdVector2 left, jdVector2 right)
{
return (float)(left.x * right.y - left.y * right.x);
}위는 2차원 벡터의 내적, 외적을 구하는 코드다. 3차원은 다르니, 3차원 벡터 내적,외적은 추후 따로 다뤄보도록 하겠다.
public static float DistanceLineAndPoint(jdVector2 s, jdVector2 e, jdVector2 p)
{
jdVector2 sp = p - s;
jdVector2 se = e - s;
jdVector2 es = s - e;
jdVector2 ep = p - e;
if(jdVector2.DotProduct(sp, se) * jdVector2.DotProduct(es,ep) >= 0)
{
return Math.Abs(jdVector2.CrossProduct(sp, se) / jdVector2.Distance(s, e));
}
else
{
return Math.Min(jdVector2.Distance(s, p), jdVector2.Distance(e, p));
}
}최종적으로 위 코드로 선분과 점 사이의 거리를 구할 수 있다.
'게임을 만들자 > 게임 서버(C#)' 카테고리의 다른 글
| 윈도우 서버 TCPNoDelay, TcpAckFrequency 설정 (1) | 2020.12.23 |
|---|---|
| c# 각도, 라디안, 벡터 간 변환 (0) | 2020.10.24 |
| c# 다각형 무게 중심 구하기 (1) | 2020.04.09 |
| c# ibatis Mapper에서 <,>,<=,>= 비교연산자 사용 (0) | 2020.04.08 |
| c# 다각형 충돌체크 (0) | 2020.02.21 |
