게임을 만들다보면 미사일과 캐릭터 같이, 오브젝트간 간 충돌 체크를 하게 된다.
원과 원, 직사각형과 원, 직사각형과 직사각형 등은 비교적 쉽게 확인이 가능하지만, 다각형 충돌체크는 방법이 쉽게 떠오르지 않는다.
여기서 다각형은 볼록한 다각형을 뜻하고, 이때 어떻게 충돌체크를 하는지 알아보자.
1. 원리
두 다각형 충돌 체크를 하는 방법은 의외로 간단하다.
(1). 두 다각형의 한 변을 선택하고,
(2). 선택한 변의 수직인 벡터로 두 다각형을 정사영 한다. (정사영이란, 도형의 각 점에서 한 평면에 내린 수선의 발이 그리는 도형)
(3). 모든 변의 수직인 벡터로 정사영 해보고, 이때 하나라도, 안 겹치는 부분이 있으면 있으면 충돌하지 않는다.
글로 보면 이해하기 어려우니 그림 예제를 보자.
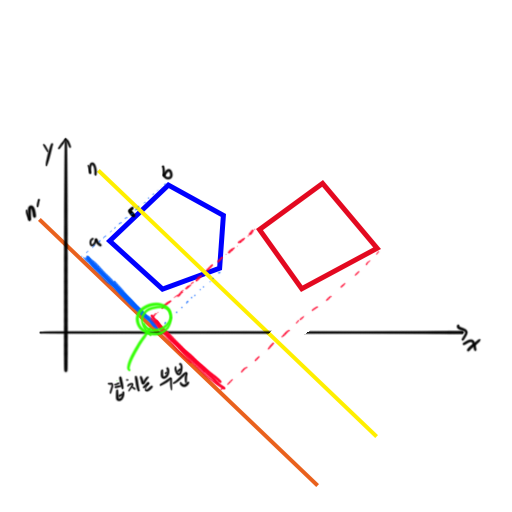
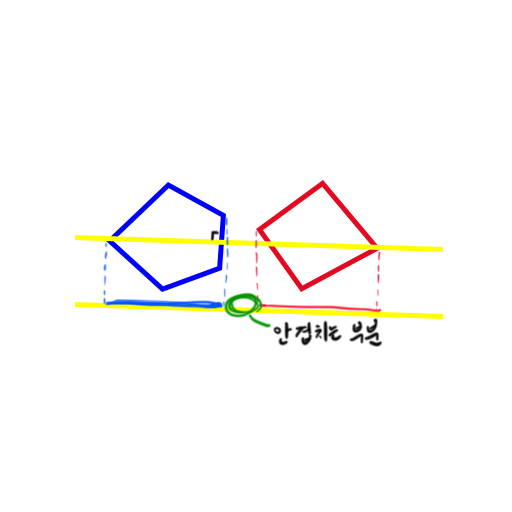
위 왼쪽 그림을 보면 알다시피, 파란 다각형의 선분ab의 [법선 벡터 n]로 두 다각형을 정사영 해 보았다. 결과는 보는 것과 같이 정사영한 부분이 겹쳐진다. 반대로 오른쪽 그림은 겹쳐지지 않는다. 이런 방법으로 두 다각형의 모든 변의 법선벡터를 구하고, 그곳으로 두 다각형을 정사영 해, 안겹쳐지는 부분이 하나라도 있으면, 충돌하지 않는다.
위의 오른쪽 그림처럼 안겹치는 부분이 있으면, 두 다각형은 충돌하지 않는다.
2. 코드
위 원리를 코드로 표현해 보자. 우선 정점을 jdVector2, 다각형을 jdPolygon으로 각각 class를 만들자.
public class jdVector2
{
public float x;
public float y;
public jdVector2()
{
x = 0;
y = 0;
}
...
}위 클래스는 보는 것과 같이 x,y좌표를 저장한다.
public class jdPolygon
{
public List<jdVector2> m_points = new List<jdVector2>();
public jdVector2 m_center = new jdVector2();
public jdPolygon()
{
}
...
}위 클래스는 다각형의 정점을 저장하기 위해, 정점들을 리스트로 관리하고 있다. m_center는 다각형의 무게 중심을 의미한다. 여기서는 쓰이지 않는다.
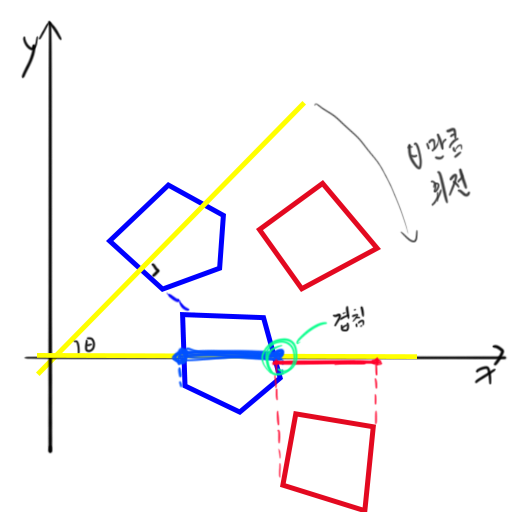
코드를 보기 전,
정사영 시키는 방법으로, 법선벡터의 각도를 구한 후(Ɵ), 각 정점을 해당 각도로 회전 시켰다. x축으로 정사영 하여 비교하는 것이 편하기 때문에, 법선 벡터 각도만큼 다각형들을 회전시킨 것이다. 두 다각형을 x축으로 정사영 한 결과가 서로 겹치는지 확인하였다.
//두 다각형의 각 변의 수직인 벡터로 정사영 한 후, 겹지는지 확인하는 함수
private bool checkProjection(jdPolygon my,jdPolygon other)
{
//삼각형 이상만 실행하도록
if(my.Points.Count < 3 || other.Points.Count < 3)
{
return false;
}
//내부에서 쓰일 임시 변수들
double tmp_radian;
double my_x1;
double my_x2;
double other_x1;
double other_x2;
double last_my_x1 = 0;
double last_my_x2 = 0;
double last_other_x1 = 0;
double last_other_x2 = 0;
double tmp_max_len = 0;
double tmp_len = 0;
double tmp_change_value;
int next_i = 0;
for(int i = 0 ; i < my.Points.Count ; i++)
{
//다음 정점의 index
next_i = (i == my.Points.Count - 1) ? 0 : i+1;
//x축을 기준으로 해당 변의 라디안를 구한다.
//이때 x좌표가 큰 쪽을 우선으로 한다.
if(my.Points[next_i].x > my.Points[i].x)
tmp_radian = Math.Atan2(my.Points[next_i].y - my.Points[i].y,
my.Points[next_i].x - my.Points[i].x);
else
tmp_radian = Math.Atan2(my.Points[i].y - my.Points[next_i].y,
my.Points[i].x - my.Points[next_i].x);
//해단 변의 각도에 90도를 더한다. 법선을 각도를 구함
tmp_radian += Math.PI * 0.5f;
//법선의 각도가 만약 60이면, -60도만큼 x축으로 회전시켜야 한다.
tmp_radian *= -1;
tmp_max_len = 0;
last_my_x1 = 0;
last_my_x2 = 0;
//각 정점을 위에서 구한 법선각도로 회전시킨다.(x축으로 회전시킨 것이라, y좌표는 0이다.
//이때 가장 작은 x값과 가장 큰 x값을 구한다.
for(int j = 0 ; j < my.Points.Count ; j++)
{
int s = (j == my.Points.Count - 1) ? 0 : j+1;
for( ; s < my.Points.Count ; s++)
{
//법선벡터 각도 만큼, 정점을 회전 시킨다.
my_x1 = my.Points[j].x*Math.Cos(tmp_radian) - my.Points[j].y*Math.Sin(tmp_radian);
my_x2 = my.Points[s].x*Math.Cos(tmp_radian) - my.Points[s].y*Math.Sin(tmp_radian);
if(my_x1 > my_x2)
{
tmp_change_value = my_x1;
my_x1 = my_x2;
my_x2 = tmp_change_value;
}
tmp_len = my_x2 - my_x1;
if(tmp_len > tmp_max_len)
{
tmp_max_len = tmp_len;
last_my_x1 = my_x1;
last_my_x2 = my_x2;
}
if(s == 0)
break;
}
}
//마찬가지로 다른 다각형을 법선 방향으로 정사영시키고,
//가장 작은 x와 가장 큰 x값을 구한다.
tmp_max_len = 0;
last_other_x1 = 0;
last_other_x2 = 0;
for(int j = 0 ; j < other.Points.Count ; j++)
{
int s = (j == other.Points.Count - 1) ? 0 : j+1;
for( ; s < other.Points.Count ; s++)
{
//법선벡터 각도 만큼, 정점을 회전 시킨다.
other_x1 = other.Points[j].x*Math.Cos(tmp_radian) - other.Points[j].y*Math.Sin(tmp_radian);
other_x2 = other.Points[s].x*Math.Cos(tmp_radian) - other.Points[s].y*Math.Sin(tmp_radian);
if(other_x1 > other_x2)
{
tmp_change_value = other_x1;
other_x1 = other_x2;
other_x2 = tmp_change_value;
}
tmp_len = other_x2 - other_x1;
if(tmp_len > tmp_max_len)
{
tmp_max_len = tmp_len;
last_other_x1 = other_x1;
last_other_x2 = other_x2;
}
if(s == 0)
break;
}
}
//각 다각형으로부터 구한 x값들이 겹치는지 확인한다.
//안겹치는 부분이 생기면, 두 다각형은 충돌하지 않는다.
if(last_my_x1 > last_other_x2 ||
last_my_x2 < last_other_x1)
return false;
}
return true;
}
public bool IsCollision(jdPolygon other)
{
return checkProjection(this, other) && checkProjection(other, this);
}모든 변을 검사해야 하기 때문에, 두 다각형을 서로 체크한다.
'게임을 만들자 > 게임 서버(C#)' 카테고리의 다른 글
| c# 다각형 무게 중심 구하기 (1) | 2020.04.09 |
|---|---|
| c# ibatis Mapper에서 <,>,<=,>= 비교연산자 사용 (0) | 2020.04.08 |
| Mysql, Select결과를 Update 문에 반영하기 (1) | 2020.02.05 |
| Mysql, Percentage 질의 구현하기 (0) | 2020.02.01 |
| 게임 서버 DB설계 시, Tips (0) | 2020.01.30 |
